Welcome to a fascinating journey into the realm of fluid dynamics, where we dive deep into understanding the velocity of a fluid particle. In this comprehensive guide, we will unravel the intricacies of fluid motion, velocity vectors, and the dynamic behavior of particles in fluid flow. Join us as we embark on this enlightening exploration.
Grasping the Basics: What is Velocity?
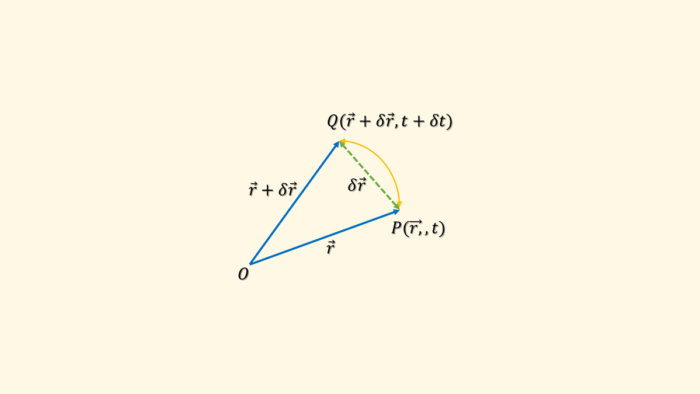
Velocity is a fundamental concept in physics that describes the rate of change of an object’s position with respect to time. In the context of fluid dynamics, velocity refers to the speed and direction of a fluid particle as it moves through space. Understanding velocity is crucial for analyzing fluid flow patterns, calculating forces, and predicting fluid behavior.
Velocity Vectors: Direction and Magnitude
When we talk about the velocity of a fluid particle, we refer to its velocity vector, which includes both magnitude (speed) and direction. Velocity vectors indicate how fast a particle is moving and in which direction it is traveling within the fluid flow field. By visualizing velocity vectors, we gain insights into the dynamic nature of fluid motion.
The Kinematics of Fluid Flow
Eulerian and Lagrangian Perspectives
In fluid dynamics, two primary perspectives are used to analyze fluid motion: Eulerian and Lagrangian. The Eulerian approach focuses on fixed points in space and observes how fluid properties change over time at those points. On the other hand, the Lagrangian approach tracks individual fluid particles as they move through space, providing a detailed view of particle trajectories and velocities.
Fluid-1Streamlines, Streaklines, and Pathlines
Streamlines, streaklines, and pathlines are visualization techniques used to represent fluid flow patterns. Streamlines show the instantaneous direction of fluid flow at each point in space, while streaklines depict the paths traced by particles released at different times. Pathlines track the actual trajectories of individual fluid particles over time, revealing their complete journey through the flow field.
The Role of Velocity in Fluid Dynamics
Reynolds Transport Theorem
The Reynolds Transport Theorem is a fundamental principle in fluid dynamics that relates the change in a fluid property (such as mass, momentum, or energy) to the local rate of change and the flux of that property through the control volume. This theorem forms the basis for analyzing fluid flow phenomena and applying conservation laws in fluid dynamics.
Bernoulli’s Equation: Balancing Forces
Bernoulli’s equation is a key concept that relates the velocity, pressure, and potential energy of a fluid particle along a streamline. It states that in an ideal, steady flow without friction, the sum of pressure energy, kinetic energy, and potential energy remains constant along the streamline. Understanding Bernoulli’s equation helps explain phenomena like lift in aerodynamics and flow in pipelines.
Types of Fluid Flow and Velocity Profiles
Laminar and Turbulent Flow
Fluid flow can be classified into laminar and turbulent based on the Reynolds number, which compares inertial forces to viscous forces in the flow. Laminar flow is characterized by smooth, orderly motion with well-defined streamlines, while turbulent flow exhibits chaotic, irregular motion with mixing and eddies. Velocity profiles vary significantly between laminar and turbulent flows.
Velocity Distribution in Pipes and Channels
In pipes and channels, fluid velocity profiles vary depending on the flow regime and boundary conditions. In laminar flow, the velocity profile is parabolic, with maximum velocity at the center and zero velocity at the walls. In turbulent flow, the velocity profile is flatter, with higher velocities near the center and lower velocities near the walls due to viscous effects.
Fluid-2Factors Influencing Fluid Particle Velocity
Viscosity and Shear Stress
Viscosity is a fluid property that determines its resistance to deformation and flow. Higher viscosity results in greater resistance, leading to slower fluid particle velocities and more pronounced viscous effects. Shear stress, generated by velocity gradients within the fluid, plays a crucial role in determining fluid behavior and flow patterns, especially in viscous fluids.
Boundary Layer and Drag
The boundary layer is a region near a solid surface where fluid velocity changes from zero at the wall to the free-stream velocity. It influences fluid particle velocities, flow separation, and drag forces experienced by objects in fluid flow. Understanding boundary layer effects is essential for optimizing designs in aerodynamics, hydrodynamics, and heat transfer applications.
Analyzing Velocity Fields: Computational Fluid Dynamics (CFD)
Introduction to CFD Simulations
Computational Fluid Dynamics (CFD) is a powerful tool used to simulate and analyze fluid flow phenomena using numerical methods. CFD software solves fluid dynamics equations, such as the Navier-Stokes equations, to predict velocity fields, pressure distributions, and flow characteristics. CFD simulations provide valuable insights into complex fluid behavior and aid in design optimization.
Applications of CFD in Engineering
CFD finds extensive applications in engineering disciplines, including aerospace, automotive, marine, and environmental engineering. It helps engineers analyze aerodynamic performance, optimize heat transfer processes, design efficient HVAC systems, and simulate fluid-structure interactions. CFD simulations enable engineers to make informed decisions and improve product performance.
Velocity Measurement Techniques
Pitot Tubes and Anemometers
Pitot tubes and anemometers are common instruments used to measure fluid velocities in various applications. Pitot tubes determine velocity by measuring the difference between stagnation pressure (total pressure) and static pressure in a fluid flow. Anemometers, such as hot-wire and vane anemometers, use different principles to measure air velocities in meteorology, HVAC systems, and wind tunnels.
Laser Doppler Velocimetry (LDV) and Particle Image Velocimetry (PIV)
Advanced techniques like Laser Doppler Velocimetry (LDV) and Particle Image Velocimetry (PIV) offer precise measurements of fluid particle velocities in complex flow fields. LDV uses laser light scattering to determine particle velocities, while PIV captures images of tracer particles to analyze flow patterns and velocity distributions. These techniques are valuable for research and engineering applications.
Real-World Applications of Fluid Particle Velocity
Aircraft Aerodynamics and Lift
In aircraft design, understanding fluid particle velocities is critical for optimizing aerodynamic performance and achieving lift. Aerodynamic forces, such as lift and drag, depend on fluid flow velocities around airfoils and wings. Engineers use computational simulations and wind tunnel tests to analyze velocity distributions and improve aircraft efficiency and stability.
Automotive Engineering and Drag Reduction
In automotive engineering, fluid particle velocities influence drag forces, fuel efficiency, and vehicle performance. Streamlining vehicle shapes, optimizing airflow around vehicles, and reducing drag coefficients depend on precise velocity measurements and flow analysis. Advanced CFD simulations and aerodynamic studies help engineers design aerodynamic vehicles and enhance fuel economy.
Conclusion: Embracing the Dynamic Nature of Fluid Particle Velocity
In conclusion, the velocity of a fluid particle is a fundamental aspect of fluid dynamics that shapes fluid behavior, flow patterns, and engineering design. By understanding velocity concepts, analyzing velocity fields, and applying measurement techniques, engineers and scientists gain valuable insights into fluid motion and optimize systems for efficiency and performance.

With havin so much content and articles do youu ever
run into any issues of plagorism oor copyright infringement?
My site has a lot of completely unique content I’ve
either created myself or outsourced but it looks like a
lot of it is popping iit up alll over the web without my
authorization. Do you know any ways to help protect against content
from being ripped off? I’d genuinely appreciate it. https://yv6Bg.mssg.me/
¡Qué onda! Mexvipdescargar es mi salvación para encontrar las apps que necesito. Descargas rápidas y sin tanto rollo. Échenle un vistazo, no se van a arrepentir. Chequen mexvipdescargar.
Taixiugamevn? Cái này thì quá quen thuộc rồi, chơi tài xỉu thì cứ phải tìm mấy trang uy tín thế này mà chơi. Đỡ bịp bợm. Safe choice taixiugamevn.
Heard some good things about 577bet1.net and decided to check it out myself. Pretty impressed! The site is easy to navigate and they have a great selection of games. Definitely worth a look. 577bet1
**mitolyn**
Mitolyn is a carefully developed, plant-based formula created to help support metabolic efficiency and encourage healthy, lasting weight management.
Thank you for your sharing. I am worried that I lack creative ideas. It is your article that makes me full of hope. Thank you. But, I have a question, can you help me?