Introduction: The Intersection of Mathematics and Nature
The Beauty of Patterns in Nature
Nature is a tapestry of patterns, from the spirals of galaxies to the symmetry of snowflakes. As a mathematician, seeing these patterns in nature offers a unique perspective on the world around us. This blog will explore the myriad ways patterns manifest in nature and how mathematics helps us understand and appreciate them.
Why Study Patterns?
Understanding patterns in nature isn’t just about appreciating beauty; it’s about uncovering the fundamental laws that govern our universe. By studying these patterns, mathematicians and scientists can make predictions, develop new technologies, and deepen our understanding of the natural world.
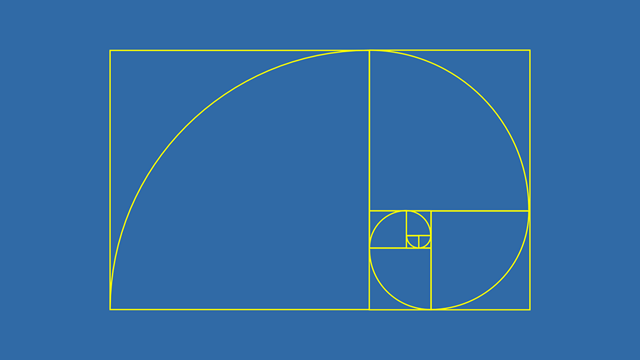
The Golden Ratio and Fibonacci Sequence
The Ubiquitous Golden Ratio
The Golden Ratio, approximately 1.618, appears in various forms in nature. From the spirals of shells to the branching of trees, this ratio is a hallmark of aesthetic beauty and structural efficiency.
Examples in Nature
You can find the Golden Ratio in the arrangement of leaves, the patterns of hurricanes, and even in the proportions of the human body. This ratio creates a sense of balance and harmony that is both visually pleasing and structurally sound.
Mathematical Explanation
The Golden Ratio is derived from the Fibonacci sequence, where each number is the sum of the two preceding ones. This sequence manifests in numerous natural phenomena, showcasing the deep connection between mathematics and the natural world.
Fibonacci Sequence in Nature
The Fibonacci sequence, starting with 0 and 1, produces a series of numbers (0, 1, 1, 2, 3, 5, 8, 13, …) that frequently appear in nature.
Examples in Plants and Animals
Sunflower seed arrangements, pine cones, and even the breeding patterns of rabbits follow the Fibonacci sequence. This sequence ensures optimal packing and efficiency, which is crucial for survival and growth.
Mathematical Insights
By understanding the Fibonacci sequence, we can gain insights into the underlying principles of growth and development in nature. This sequence highlights how simple mathematical rules can lead to complex and beautiful structures.
Fractals: Infinite Complexity
The Concept of Fractals
Fractals are geometric shapes that can be split into parts, each of which is a reduced-scale copy of the whole. This property, known as self-similarity, is a key characteristic of fractals.
Natural Fractals
You can find fractals in various natural structures, such as the branching patterns of trees, the structure of snowflakes, and the rugged coastline of continents. These patterns repeat at different scales, creating infinite complexity from simple rules.
Mathematical Foundations
The mathematics of fractals involves iterative processes and complex numbers. Fractals like the Mandelbrot set illustrate how simple mathematical formulas can produce infinitely intricate patterns.
Fractals in Ecosystems
Fractals aren’t just limited to physical structures; they also appear in ecological systems. The distribution of plants, the branching of rivers, and the structure of ecosystems all exhibit fractal patterns.
Examples and Applications
By studying fractals, ecologists can better understand the complexity of ecosystems and develop strategies for conservation and management. Fractals help us see the interconnectedness and scalability of natural systems.
Symmetry in Nature
Types of Symmetry
Symmetry is a fundamental aspect of patterns in nature. There are various types of symmetry, including rotational, reflective, and translational.
Rotational Symmetry
Rotational symmetry is seen in flowers, starfish, and many other natural forms. This type of symmetry involves rotating an object around a central point and finding that it looks the same at various angles.
Reflective Symmetry
Reflective symmetry, where one half of an object is a mirror image of the other, is common in animals and plants. This type of symmetry is crucial for balance and function in living organisms.
Symmetry and Evolution
Symmetry plays a significant role in evolution and natural selection. Symmetrical features often indicate health and genetic fitness, making them attractive traits in the animal kingdom.
Mathematical Perspective
By analyzing symmetry mathematically, we can understand how these patterns contribute to the survival and reproduction of species. Symmetry also helps in the study of biological development and the mechanics of movement.
Tessellations: Tiling the Plane
Definition of Tessellations
Tessellations are patterns formed by repeating shapes without gaps or overlaps. These patterns are common in both man-made and natural structures.
Examples in Nature
Honeycombs, turtle shells, and certain types of crystals exhibit tessellation patterns. These arrangements maximize space efficiency and structural integrity.
Mathematical Explanation
Mathematically, tessellations involve geometric shapes and transformations. Understanding these patterns helps in various fields, from architecture to materials science.
Applications of Tessellations
Tessellations have practical applications in designing materials and structures. By mimicking natural tessellations, engineers can create stronger, more efficient designs.
Biological Significance
In biology, tessellations can be seen in cellular structures and tissue organization. These patterns ensure optimal function and resource allocation in living organisms.
Spirals: Nature’s Elegant Curves
The Prevalence of Spirals
Spirals are one of the most common patterns in nature, found in galaxies, hurricanes, shells, and plants. These elegant curves are not only beautiful but also functional.
Examples in Plants and Animals
The nautilus shell, sunflower heads, and spiral galaxies all follow logarithmic spiral patterns. These patterns optimize growth, energy distribution, and structural integrity.
Mathematical Foundations
Logarithmic spirals can be described mathematically using polar coordinates. This mathematical understanding helps explain why spirals are so prevalent in nature.
Spirals and Efficiency
Spirals are efficient for packing and growth. They allow organisms to grow in a compact, organized manner, making the best use of space and resources.
Practical Applications
Understanding spirals can help in fields like engineering and architecture. By mimicking these natural patterns, we can create more efficient and aesthetically pleasing designs.
Chaos Theory: Finding Order in Disorder
The Basics of Chaos Theory
Chaos theory studies systems that appear random but are governed by underlying patterns and deterministic laws. This field of mathematics helps explain the unpredictability in natural systems.
Examples in Nature
Weather patterns, animal populations, and even the stock market exhibit chaotic behavior. These systems are sensitive to initial conditions, leading to complex, seemingly random outcomes.
Mathematical Insights
By using mathematical models, scientists can identify the underlying patterns in chaotic systems. This understanding helps in predicting and managing complex systems.
Chaos and Fractals
Chaos theory is closely related to fractals. Many chaotic systems exhibit fractal structures, showing self-similarity and infinite complexity.
Practical Applications
Chaos theory has applications in various fields, including meteorology, biology, and economics. By understanding chaos, we can better manage and predict complex systems.
Wave Patterns: Harmony in Motion
The Nature of Waves
Waves are a fundamental pattern in nature, from the ripples on a pond to the light we see. Understanding wave patterns helps us grasp the behavior of various natural phenomena.
Examples in Nature
Ocean waves, sound waves, and electromagnetic waves all follow similar principles. These patterns involve oscillations and energy transfer.
Mathematical Foundations
Wave patterns can be described using mathematical equations, such as the sine and cosine functions. This mathematical framework helps in analyzing and predicting wave behavior.
Waves and Interference
Waves can interact through interference, leading to complex patterns. This interaction can be constructive or destructive, creating areas of amplification or cancellation.
Practical Applications
Understanding wave patterns has practical applications in fields like acoustics, optics, and telecommunications. By studying waves, we can develop better technologies for communication and imaging.
The Hexagon: Nature’s Perfect Shape
The Efficiency of Hexagons
Hexagons are a common pattern in nature, known for their efficiency and strength. This shape is found in various natural structures, from honeycombs to crystals.
Examples in Nature
Honeybees use hexagonal cells in their hives to maximize space and structural integrity. Snowflakes and certain minerals also form hexagonal patterns.
Mathematical Explanation
Hexagons are the most efficient shape for tiling a plane without gaps. This efficiency makes them a preferred pattern in natural and man-made structures.
Hexagons and Structural Strength
Hexagons provide structural strength, making them ideal for building robust structures. This pattern distributes stress evenly, enhancing durability.
Practical Applications
Engineers and architects often use hexagonal patterns in design for their efficiency and strength. Understanding these patterns helps in creating more sustainable and resilient structures.
Branching Patterns: Nature’s Network
The Prevalence of Branching
Branching patterns are ubiquitous in nature, seen in trees, rivers, and blood vessels. These patterns optimize resource distribution and connectivity.
Examples in Plants and Animals
Trees and plants use branching patterns to maximize light exposure and nutrient absorption. Rivers and streams form branching networks for efficient water flow.
Mathematical Insights
Branching patterns can be described using fractals and network theory. This mathematical understanding helps in analyzing and modeling natural systems.
Branching and Efficiency
Branching patterns are efficient for distributing resources and connecting different parts of a system. This efficiency is crucial for survival and growth in nature.
Practical Applications
By mimicking branching patterns, engineers can design more efficient networks and systems. This approach is used in fields like transportation, communication, and biology.
Patterns in Animal Markings
The Diversity of Animal Markings
Animal markings, from stripes to spots, exhibit a wide range of patterns. These markings serve various functions, including camouflage, communication, and mating.
Examples in the Animal Kingdom
Tigers have stripes for camouflage in tall grass, while peacocks use vibrant patterns for attracting mates. These markings are not just random; they follow specific patterns.
Mathematical Models
Mathematicians use models like reaction-diffusion systems to explain the formation of animal markings. These models help in understanding how patterns develop and evolve.
Functions of Animal Markings
Animal markings play crucial roles in survival and reproduction. By studying these patterns, scientists can gain insights into the behavior and evolution of species.
Practical Applications
Understanding animal markings can aid in conservation efforts and the study of biodiversity. It also has applications in biomimicry, where natural patterns inspire new technologies.
The Role of Symmetry in Crystal Formation
Crystal Symmetry
Crystals are renowned for their symmetrical patterns, which result from the orderly arrangement of atoms. This symmetry is a fundamental aspect of crystallography.
Examples in Minerals
Quartz, salt, and diamonds all exhibit symmetrical crystal structures. These patterns are not just visually striking; they also determine the properties of the crystals.
Mathematical Explanation
The mathematics of symmetry groups helps in understanding crystal structures. This knowledge is essential in fields like materials science and chemistry.
Symmetry and Material Properties
The symmetry of crystals affects their physical and chemical properties. By studying these patterns, scientists can develop new materials with desired characteristics.
Practical Applications
Crystal symmetry has applications in electronics, optics, and pharmaceuticals. Understanding these patterns helps in designing better materials and devices.
Patterns in Weather Systems
The Dynamics of Weather Patterns
Weather systems exhibit complex patterns, from swirling hurricanes to jet streams. These patterns result from the interaction of various atmospheric factors.
Examples of Weather Patterns
Hurricanes, tornadoes, and cyclones are examples of large-scale weather patterns. These systems follow specific paths and exhibit characteristic shapes.
Mathematical Models
Mathematical models, such as differential equations and chaos theory, help in understanding and predicting weather patterns. These models account for the dynamic and interconnected nature of the atmosphere.
Predicting Weather
By analyzing weather patterns, meteorologists can make more accurate predictions. This knowledge is crucial for preparing for and mitigating the impacts of extreme weather events.
Practical Applications
Understanding weather patterns has practical applications in agriculture, disaster management, and climate science. Accurate weather predictions help in planning and decision-making.
Patterns in Human Behavior
The Mathematics of Social Patterns
Human behavior, from traffic flow to social networks, exhibits patterns that can be analyzed mathematically. These patterns provide insights into how individuals and groups interact.
Examples in Daily Life
Traffic congestion, voting behavior, and the spread of information all follow specific patterns. By studying these patterns, we can understand and influence social dynamics.
Mathematical Models
Models like graph theory and game theory help in analyzing social patterns. These mathematical tools provide a framework for studying complex human behavior.
Predicting and Influencing Behavior
By understanding patterns in human behavior, we can make better decisions in fields like public policy, marketing, and urban planning. This knowledge helps in creating more efficient and equitable systems.
Practical Applications
Analyzing social patterns has applications in various fields, including sociology, economics, and public health. Understanding these patterns helps in addressing social issues and improving quality of life.
The Role of Patterns in Music
Mathematical Patterns in Music
Music is a blend of rhythm, melody, and harmony, all of which follow mathematical patterns. These patterns create the structure and beauty of musical compositions.
Examples in Musical Compositions
From the beats of a drum to the scales of a piano, music is filled with patterns. Composers use mathematical principles to create harmony and balance in their works.
Mathematical Foundations
Mathematics helps in understanding the structure of music, from the ratios of musical intervals to the symmetry of compositions. This knowledge enhances our appreciation of music.
Patterns and Musical Creativity
Understanding patterns in music can inspire creativity and innovation. By studying these patterns, musicians can develop new styles and techniques.
Practical Applications
Mathematical patterns in music have applications in fields like music theory, acoustics, and digital signal processing. This knowledge helps in creating better musical instruments and technologies.
Patterns in Art and Architecture
The Influence of Patterns
Art and architecture are deeply influenced by patterns, from the symmetry of buildings to the fractals in paintings. These patterns create aesthetic appeal and structural integrity.
Examples in Art and Architecture
The geometric patterns of Islamic art, the symmetry of classical architecture, and the fractals in modern art all showcase the influence of patterns.
Mathematical Insights
Mathematics provides a framework for understanding and creating patterns in art and architecture. This knowledge helps in designing more beautiful and functional works.
Patterns and Aesthetic Appeal
Patterns create a sense of order and harmony, enhancing the aesthetic appeal of art and architecture. By studying these patterns, artists and architects can create more impactful works.
Practical Applications
Understanding patterns in art and architecture has applications in design, urban planning, and cultural studies. This knowledge helps in preserving and innovating artistic traditions.
Patterns in Financial Markets
The Dynamics of Financial Patterns
Financial markets exhibit patterns in price movements, trading volumes, and investor behavior. These patterns help in understanding and predicting market trends.
Examples in Financial Markets
Stock prices, exchange rates, and commodity prices all follow specific patterns. By analyzing these patterns, traders and investors can make informed decisions.
Mathematical Models
Mathematical models, such as stochastic processes and fractals, help in analyzing financial patterns. These models provide insights into market dynamics and risk management.
Predicting Market Trends
By understanding patterns in financial markets, analysts can make better predictions and develop effective investment strategies. This knowledge is crucial for financial planning and risk management.
Practical Applications
Analyzing financial patterns has applications in fields like economics, finance, and business. Understanding these patterns helps in making more informed and strategic decisions.
Patterns in Language
The Structure of Language
Language is filled with patterns, from the grammar of sentences to the rhythm of poetry. These patterns create the structure and meaning of communication.
Examples in Linguistics
Phonetic patterns, syntactic structures, and semantic relationships all follow specific rules. By studying these patterns, linguists can understand the nature of language.
Mathematical Foundations
Mathematics helps in analyzing the patterns of language, using tools like formal grammars and information theory. This knowledge enhances our understanding of communication.
Patterns and Language Learning
Understanding patterns in language can aid in language learning and translation. By recognizing these patterns, learners can acquire new languages more effectively.
Practical Applications
Analyzing language patterns has applications in fields like linguistics, artificial intelligence, and education. This knowledge helps in developing better language technologies and teaching methods.
Patterns in Medicine
The Role of Patterns in Health
Medicine relies on patterns to diagnose diseases, understand physiological processes, and develop treatments. These patterns provide insights into the functioning of the human body.
Examples in Medical Science
Patterns in symptoms, genetic sequences, and epidemiological data all play a role in medical research. By studying these patterns, doctors can improve patient care.
Mathematical Models
Mathematical models, such as differential equations and statistical analysis, help in understanding medical patterns. These models provide a framework for predicting and managing health conditions.
Patterns and Disease Prevention
By recognizing patterns in medical data, researchers can develop strategies for disease prevention and control. This knowledge is crucial for public health and medical practice.
Practical Applications
Understanding patterns in medicine has applications in fields like healthcare, pharmaceuticals, and biotechnology. This knowledge helps in improving diagnosis, treatment, and prevention.
Patterns in Technology
The Influence of Patterns
Technology is deeply influenced by patterns, from the algorithms of software to the circuits of hardware. These patterns create efficiency and functionality in technological systems.
Examples in Technology
Pattern recognition in artificial intelligence, circuit design in electronics, and data structures in computer science all showcase the influence of patterns.
Mathematical Insights
Mathematics provides a framework for understanding and creating patterns in technology. This knowledge helps in developing more advanced and efficient technologies.
Patterns and Innovation
Understanding patterns in technology can inspire innovation and problem-solving. By studying these patterns, technologists can develop new tools and applications.
Practical Applications
Analyzing patterns in technology has applications in fields like engineering, computer science, and information technology. Understanding these patterns helps in creating better technologies and systems.
Patterns in Astronomy
The Cosmic Patterns
Astronomy reveals patterns in the distribution of stars, the structure of galaxies, and the motion of celestial bodies. These patterns help in understanding the universe.
Examples in Astronomy
The spiral arms of galaxies, the regular orbits of planets, and the periodicity of celestial events all follow specific patterns. By studying these patterns, astronomers can uncover the mysteries of the cosmos.
Mathematical Models
Mathematical models, such as gravitational equations and statistical analysis, help in analyzing astronomical patterns. These models provide insights into the dynamics and evolution of the universe.
Patterns and Cosmic Understanding
Understanding patterns in astronomy can deepen our knowledge of the cosmos and our place in it. This knowledge helps in exploring the universe and developing new technologies.
Practical Applications
Analyzing patterns in astronomy has applications in fields like astrophysics, space exploration, and cosmology. Understanding these patterns helps in advancing our knowledge of the universe.
FAQs
- What are patterns in nature?
- Patterns in nature are regular, repeated forms or designs found in natural objects and phenomena.
- How do mathematicians study patterns in nature?
- Mathematicians use models, equations, and theories to analyze and understand the underlying principles of natural patterns.
- What is the Golden Ratio?
- The Golden Ratio is a mathematical ratio, approximately 1.618, often found in nature and associated with aesthetic beauty and structural efficiency.
- What are fractals?
- Fractals are complex geometric shapes that exhibit self-similarity at different scales, often found in natural structures like coastlines and trees.
- How do symmetry patterns benefit living organisms?
- Symmetry patterns provide balance and functionality, often indicating health and genetic fitness, crucial for survival and reproduction.
- Why are spirals common in nature?
- Spirals optimize growth, energy distribution, and structural integrity, making them an efficient pattern for many natural forms.
- What is chaos theory?
- Chaos theory studies systems that appear random but are governed by underlying patterns and deterministic laws, explaining the unpredictability in natural systems.
- How do branching patterns benefit ecosystems?
- Branching patterns optimize resource distribution and connectivity, essential for growth and survival in ecosystems.
- What role do patterns play in human behavior?
- Patterns in human behavior provide insights into social dynamics, helping in fields like public policy, marketing, and urban planning.
- How do patterns influence art and architecture?
- Patterns create aesthetic appeal and structural integrity, deeply influencing design and cultural expression in art and architecture.
Add a Comment