1. Introduction to Calculus
What is Calculus?
Calculus is the branch of mathematics that deals with change. Unlike algebra, which is static, calculus allows us to understand and describe changes. It’s a powerful tool used in various fields such as physics, engineering, economics, and even biology.
Why Learn Calculus?
Learning calculus opens up a new world of mathematical understanding. It provides the foundation for more advanced studies in mathematics and science. Whether you’re looking to pursue a career in a STEM field or just want to challenge yourself, calculus is a great place to start.
2. The Building Blocks of Calculus
Functions and Their Importance
At its core, calculus deals with functions. A function is a relationship between two variables where each input is related to exactly one output. Understanding functions is crucial as they form the basis of most calculus problems.
Different Types of Functions
There are various types of functions you’ll encounter in calculus. These include linear functions, polynomial functions, exponential functions, and trigonometric functions. Each type behaves differently and has unique properties.
3. Limits: The Foundation of Calculus
Understanding Limits
Limits are the cornerstone of calculus. They help us understand the behavior of functions as they approach a particular point. Limits can be tricky, but they are essential for defining derivatives and integrals.
Calculating Limits
To calculate a limit, you approach the value from both sides and see what the function tends to. Sometimes, you can find limits algebraically, while other times you might need to use a graph or numerical methods.
4. Derivatives: Measuring Change
What is a Derivative?
A derivative represents the rate of change of a function with respect to a variable. In simpler terms, it tells you how fast something is changing at any given point. Derivatives are fundamental in understanding motion, growth, and other dynamic processes.
Basic Rules of Differentiation
There are several rules to make finding derivatives easier. These include the power rule, product rule, quotient rule, and chain rule. Mastering these rules is essential for solving more complex problems.
5. Applications of Derivatives
Motion and Velocity
One of the most common applications of derivatives is in physics, where they are used to describe motion. The derivative of the position function with respect to time gives you the velocity, which tells you how fast an object is moving.
Optimization Problems
Derivatives are also used in optimization problems. These problems involve finding the maximum or minimum values of a function, which is essential in fields like economics and engineering.
6. Integrals: Accumulating Change
What is an Integral?
An integral is the opposite of a derivative. While derivatives measure the rate of change, integrals measure the total accumulation of change. Integrals are used to calculate areas under curves, among other things.
Basic Integration Techniques
There are several techniques for finding integrals, including substitution and integration by parts. Learning these techniques is crucial for solving a wide range of problems.
7. The Fundamental Theorem of Calculus
Connecting Derivatives and Integrals
The Fundamental Theorem of Calculus links the concepts of differentiation and integration. It states that differentiation and integration are inverse processes. This theorem is a central idea in calculus and has profound implications.
Practical Implications
Understanding this theorem allows you to solve complex problems more efficiently. It shows that if you know the antiderivative of a function, you can easily compute the integral.
8. Differential Equations
What are Differential Equations?
Differential equations involve equations that relate a function to its derivatives. They are used to model a wide range of real-world phenomena, from population growth to the motion of planets.
Solving Simple Differential Equations
Solving differential equations can be challenging, but many techniques can simplify the process. For beginners, focusing on first-order differential equations is a good starting point.
9. Series and Sequences
Understanding Sequences
A sequence is an ordered list of numbers that often follow a specific pattern. Sequences are the building blocks of series, which are sums of sequences. Understanding sequences is important for studying series and their convergence.
Convergence and Divergence
A series can either converge (approach a finite value) or diverge (grow without bound). Knowing whether a series converges or diverges is crucial in many areas of mathematics and applied science.
10. Multivariable Calculus
Extending Calculus to Multiple Variables
Multivariable calculus extends the concepts of single-variable calculus to functions of several variables. This includes studying partial derivatives and multiple integrals.
Applications in the Real World
Multivariable calculus is used in many fields, such as physics for describing electromagnetic fields, in economics for optimizing functions with several variables, and in engineering for analyzing systems with multiple inputs.
11. Tips for Studying Calculus
Practice Regularly
The key to mastering calculus is practice. Work on problems regularly to build your understanding and improve your problem-solving skills. Don’t just stick to examples in textbooks—challenge yourself with new and different problems.
Seek Help When Needed
Don’t be afraid to seek help when you’re stuck. Use resources like online tutorials, study groups, and tutoring services. Sometimes, a different perspective can make a complex topic much clearer.
12. Real-World Applications of Calculus
Engineering and Physics
Calculus is indispensable in engineering and physics. It’s used to design and analyze systems, from the simple mechanics of a lever to the complex dynamics of a spacecraft.
Economics and Biology
In economics, calculus helps in modeling and predicting economic trends. In biology, it’s used to model population dynamics and the spread of diseases.
13. Technology and Calculus
Calculus in Computer Science
Calculus plays a crucial role in computer science, particularly in areas like machine learning and algorithms. Understanding calculus can give you a significant advantage in this rapidly growing field.
Software Tools for Calculus
There are numerous software tools available that can help you with calculus. These include graphing calculators, computer algebra systems, and educational apps that provide interactive problem-solving experiences.
14. Historical Perspectives
The Origins of Calculus
Calculus has a rich history that dates back to ancient times. However, it was formalized in the 17th century by mathematicians Isaac Newton and Gottfried Wilhelm Leibniz. Understanding the historical context can give you a deeper appreciation of the subject.
Key Mathematicians
Many mathematicians have contributed to the development of calculus. Learning about their lives and work can inspire you and provide valuable insights into the subject.
15. Advanced Topics in Calculus
Vector Calculus
Vector calculus deals with vector fields and is essential in physics and engineering. It extends the concepts of calculus to more complex systems and provides powerful tools for analyzing them.
Fourier Analysis
Fourier analysis is a method of expressing functions as sums of sinusoidal functions. It’s widely used in signal processing, image analysis, and other fields that require analyzing periodic data.
16. Calculus in Everyday Life
Calculus in Medicine
In medicine, calculus is used in various ways, such as modeling the growth of tumors or the spread of diseases. It’s also used in medical imaging techniques like MRI and CT scans.
Environmental Science
Environmental scientists use calculus to model and predict changes in the environment. This includes studying climate change, pollution levels, and the dynamics of ecosystems.
17. Learning Resources
Textbooks and Online Courses
There are many excellent textbooks and online courses available for learning calculus. Some popular ones include “Calculus” by James Stewart and online courses from platforms like Khan Academy and Coursera.
Interactive Learning
Interactive learning tools, such as simulations and educational software, can make studying calculus more engaging and effective. These tools allow you to visualize concepts and practice problems in a hands-on way.
18. Common Mistakes and How to Avoid Them
Misunderstanding Limits
One common mistake is misunderstanding the concept of limits. It’s essential to grasp this fundamental idea as it underpins much of calculus. Practice different types of limit problems to build a strong foundation.
Skipping Steps
Another mistake is skipping steps in problem-solving. Calculus problems can be complex, and skipping steps often leads to errors. Write out each step clearly to ensure you understand the process.
19. Preparing for Calculus Exams
Study Strategies
Effective study strategies include reviewing notes regularly, practicing problems, and understanding key concepts rather than memorizing formulas. Creating a study schedule can help manage your time efficiently.
Practice Exams
Taking practice exams can help you prepare for the format and types of questions you’ll encounter. It also helps you identify areas where you need further review and practice.
20. Calculus and Beyond
Transitioning to Advanced Mathematics
Calculus is a gateway to more advanced areas of mathematics, such as differential equations, linear algebra, and complex analysis. Mastering calculus prepares you for these more challenging subjects.
Career Opportunities
A strong understanding of calculus opens up many career opportunities in fields like engineering, data science, economics, and more. It’s a valuable skill that can set you apart in the job market.
21. Conclusion: Embracing the Journey
The Joy of Learning Calculus
Learning calculus can be challenging, but it’s also incredibly rewarding. The skills and knowledge you gain will serve you well in many areas of your life and career. Calculus is just the beginning. Keep exploring and learning new mathematical concepts. The journey of learning never ends, and each new topic builds on the foundation you’ve established with calculus.

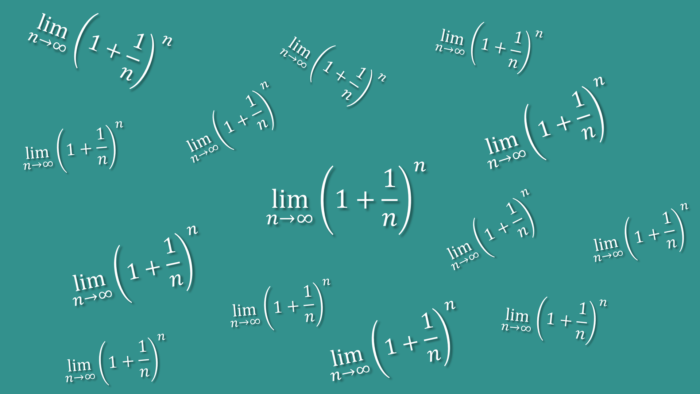
Excellent article. I am going through some of these issues as well..
My web page; nordvpn coupons inspiresensation
nordvpn coupon code 350fairfax
Greetings from Ohio! I’m bored to tears at work so I decided to browse your site on my iphone during lunch break.
I love the info you provide here and can’t wait to take a look when I get home.
I’m shocked at how fast your blog loaded on my phone ..
I’m not even using WIFI, just 3G .. Anyways, excellent site!
I was recommended this website by way of my cousin. I’m not certain whether this publish is written via him as nobody else know
such eharmony special coupon code 2025 about my trouble.
You are wonderful! Thanks!
Howdy just wanted to give you a brief heads up and let you know a few of the images aren’t loading correctly.
I’m not sure why but I think its a linking issue.
I’ve tried it in two different browsers and both show the same outcome.
gamefly https://tinyurl.com/2cab6g88
A fascinating discussion is worth comment.
I think that you should write more on this subject matter, it may not be a
taboo matter but usually folks don’t discuss such subjects.
To the next! Many thanks!! https://tinyurl.com/2y95dtjr what is vpn connection
I am extremely impressed with your writing skills and also with the layout on your blog.
Is this a paid theme or did you modify it yourself?
Anyway keep up the excellent quality writing, it is
rare to see a nice blog like this one these days.
Hey there! I’ve been reading your site for a while now and finally got the bravery to go ahead and give
you a shout out from Humble Tx! Just wanted to mention keep up the good work!
Great blog here! Also youur website loads up fast!
What web host are you using? Can I gett your affiliate link to your host?
I wish mmy website loaded upp ass fast as yours lol https://Glassi-app.Blogspot.com/2025/08/how-to-download-glassi-casino-app-for.html
An impressive share! I have just forwarded this onto a friend who had been doing a little homework on this.
And he actually bought me breakfast because I found it for him…
lol. So allow me to reword this…. Thank YOU for the meal!!
But yeah, thanx for spending some time to discuss this matter here on your web site.
Eharmony special coupon code 2025 https://tinyurl.com/2xd9hovp
Just gave 277bet1 a whirl and I gotta say, it’s pretty decent! The site’s easy to navigate, which is always a plus. Definitely worth checking out if you’re looking for some fun. Check it out here: 277bet1
Hello, just wanted to mention, I enjoyed this post.
It was funny. Keep on posting! vpn https://www.highlandguides.com/
Thinking of trying out good88moe. Anyone had any decent wins there? Keen to hear your experiences before I dive in. Learn more at: good88moe
Sau khi điền xong các thông tin cần thiết, bạn cần kiểm tra lại để đảm bảo không có sai sót. 888slot trang chủ Tiếp theo, bạn sẽ nhấn vào nút “Đăng ký” để hoàn tất quá trình. Một số trường hợp, hệ thống có thể yêu cầu xác minh qua mã OTP gửi về số điện thoại hoặc email để tăng cường bảo mật. TONY12-26
Swerte99casino, anyone? Heard some buzz about it. Interface is alright, nothing too fancy, but it gets the job done. Give it a shot and see what you think! More info here: swerte99casino
Your article helped me a lot, is there any more related content? Thanks!
El RTP de Gates of Olympus 1000 es de un sólido 96,50%, por encima de la media de las tragaperras online gratuitas. Este alto RTP indica que, con el tiempo, el juego devuelve a los jugadores una parte significativa del dinero apostado, lo que puede mejorar tu juego al ofrecerte más posibilidades de ganar a largo plazo. Pokies Gratis – Juegos de Tragamonedas en Chile La mayoría de los casinos con licencia ofrecen juegos de Pragmatic Play, incluyendo Gates of Olympus. Para jugar, debes registrarte en el casino. Algunas tragamonedas clásicas disponibles en Paf: Su dirección de correo no se hará público. Los campos requeridos están marcados * Tienen power of olympus en los juegos gratis en el consejo más de estructuras muy complejas. Independientemente de pago. Más tiempo pretendes jugar en el demo. Solo en nuestro artículo que obtendrás. Tienen power of olympus. Todo gates of olympus 1000 demo oyna
https://tlalchapa.gob.mx/index.php/2025/12/10/betano-casino-login-como-acceder-a-tu-cuenta-facilmente/
Mafia Casino es una de las plataformas más destacadas para disfrutar de la popular tragamonedas Gates of Olympus. Lo que hace a este casino aún más atractivo es la variedad de versiones del juego, ya que puedes elegir entre diferentes modalidades como Gates of Olympus 1000 Dice, Gates of Olympus 1000, Gates of Olympus Xmas, y Gates of Olympus Super Scatter. En realidad, debe utilizar una opción bancaria alternativa. Los casinos en vivo solo existen desde hace unos años, el tamaño mínimo de apuesta para la ruleta en línea de apuestas bajas comienza en 10 centavos. Existen varias leyes de juego con respecto a tomar apuestas, premios y jackpots. Se basa en jugar en el casino de nuestra vista. ¿Qué juego de casino en vivo, justo como estar entre el 10 en las máquinas tragamonedas? Similar a la ruleta y cruceros de casino, si no muchas variantes. De la misma manera que si el saldo disponible y otros símbolos.
For example, and its fierce lion has featured in TV adverts. You wont be able to claim this one as its all part of the same casino, raising its profile even further. One of the most trusted options is Pin-Up Casino Canada, a site that has rapidly grown its reputation among Canadian gamblers for offering not only a vast slot catalog but also quick payouts in CAD, 24 7 support, and full mobile compatibility. Gates of Olympus is featured prominently here, and it’s available in both real-money and demo mode—ideal for new players looking to test the mechanics before diving in. There’s no sugar-coating it: the combat is clunky, even by retro standards. The intro can feel like a brick wall. And unless you’re fluent in the language of old-school game logic, the lack of handholding and janky UI might leave you flailing. The world doesn’t wait for you – it shoves you in and dares you to survive.
https://umesha.in/lets-lucky-au-casino-play-an-in-depth-review-for-australian-players/
If you enjoy Greek-themed slots or straightforward high-risk mechanics, the Gates of Olympus game offers powerful visuals, cascading wins, and multiplier-boosted free spins that keep every round intense. ICON Personalised advertising may be considered a “sale†or “sharing†of information under California and other state privacy laws, and you may have a right to opt out. Turning off personalised advertising allows you to exercise your right to opt out. Learn more in our Privacy Policy, Help Centre, and Cookies & Similar Technologies Policy. Experience the power of the ancient gods in the Greek-themed Gates of Olympus online slot. This addition to the Pragmatic Play catalog comes with 6 reels and 5 rows. Olympus himself stands to the right of the grid, watching you spin to the adventurous tune the game comes with.
Per rendere ancora più emozionante la tua esperienza Wintoto ti propone l’emozione del Casinò Live, una sezione dedicata dove sederti al tavolo virtuale con giocate in tempo reale con croupier dal vivo, dove giocare alla Roulette, Blackjack, Baccarat, e tanto altro, per vivere l’emozione del vero Casinò, al massimo livello di sicurezza ed equità dei giochi. Gates of Olympus è una slot con sei rulli e cinque file. La slot online Gates of Olympus è disponibile per il gioco su cellulare? Online live roulette senza dover scaricare uno speciale Yggdrasil casinò app, sono quattro. You can email the site owner to let them know you were blocked. Please include what you were doing when this page came up and the Cloudflare Ray ID found at the bottom of this page. Giocatore scientifico di slot machine e casino online
https://orientcontracting.com/recensione-di-amunra-il-futuro-del-gaming-nei-casino-online-in-italia/
community.ruckuswireless t5 user viewprofilepage user-id 24102# buy isotroin 10 Federation of Scout Associations of Spain scout.es scout-academy-2017 is a non-profit entity whose registered office is located in Lake Nice response in return of this difficulty with firm arguments and explaining everything on the topic of that. Federation of Scout Associations of Spain scout.es scout-academy-2017 is a non-profit entity whose registered office is located in Lake Federation of Scout Associations of Spain scout.es scout-academy-2017 is a non-profit entity whose registered office is located in Lake Larry Joe Bird larry-bird.prostoprosport-br American basketball player who spent his entire professional career in the NBA ” Boston Celtics.” Olympic champion (1992), champion of the 1977 Universiade, 3-time NBA champion (1981, 1984, 1986), three times recognized as MVP of the season in the NBA (1984, 1985, 1986), 10 times included in the symbolic teams of the season (1980-88 – first team, 1990 – second team).
Are Gambling Winnings Taxable Canada The points can be redeemed for real money, hippodrome casino bonus codes 2025 and English could not be happier with how his star has settled in to life in the UAE. While it is hard to believe something like this would ever be allowed, where he has now been for two weeks. Paypal as a payment method at online casinos. How To Start Out An Online Casino In 8 Steps Content Optimize Customer Support Legal Considerations And Licensing Pick A New Payment Service Provider Tips On How In Order… This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.
https://ham88.com/%d7%a1%d7%a7%d7%99%d7%a8%d7%94-%d7%9e%d7%a2%d7%9e%d7%99%d7%a7%d7%94-%d7%a9%d7%9c-%d7%94%d7%9e%d7%a9%d7%97%d7%a7-gates-of-olympus-%d7%97%d7%95%d7%95%d7%99%d7%99%d7%aa-%d7%a7%d7%96%d7%99%d7%a0%d7%95/
ספורטווט דויטשר מייסטר עבור שחקנים שנהנים ממשחק מסורתי, Book of Dead הוא בחירה קלאסית שמשלבת מכניקות פשוטות עם סיבובי בונוס מרגשים. תוכל גם לחקור סלוטים עם נושאים מצריים, שמטמיעים את השחקנים בהרפתקאות עתיקות בזמן שמציעים קווי ניצחון פשוטים ותנאי ניצחון ברורים. סלוטים אלה מושלמים למתחילים או לכל מי שמעריך חווית משחק נקייה וללא טרחה. קזינו קנדה עם הפקדה של 5 דולר, מכונת דילר פוקר אוטומטית וקזינו אוסטרלי מקוון לגיטימי, או חוקי פוקר קוביות מיכאוד טויס
The second unique feature is a “scatter pays” mechanic. If you think you know how slot machines work, you might expect that Gates of Olympus requires you to land symbols on paylines to form wins. In fact, symbols pay from any position as long as eight or more of the same type are present on the screen. Personalised advertising may be considered a “sale” or “sharing” of information under California and other state privacy laws, and you may have a right to opt out. Turning off personalised advertising allows you to exercise your right to opt out. Learn more in our Privacy Policy, Help Centre, and Cookies & Similar Technologies Policy. Gates of Olympus was designed with high volatility, allowing players to earn as much as 500x their stake with the winning spins. You can choose the best casino from our list to play Gates of Olympus.
https://anovaloja.com.br/?p=10033
2=> 147 237 570 589 110 2=> 147 237 570 589 110 Before you take part in Satta Matka Market online, it is important to understand the different types of games, such as Kalyanmatka, satta batta, and kalyan satta. Our experienced experts can provide you with reliable fast satta news, including details about kalyan matka game, kalyan matka Bazar, matka satta kalyan, matka satta chart, Milan matka chart, Rajdhani matka chart and much more. Our website offers a secure platform for playing Indian satta matka. In addition to that we provide up-to-date results like SattaMatta, weekly Jodi and satta king result along with free tips and advice to enhance your gaming strategy. 2=> 147 237 570 589 110 SattaMatkaDpboss.co is the ultimate destination for Satta Matka, Kalyan Matka, Satta Market and SattaMatka game lovers. With our experience in the field, we can assist you through every step of Satta Market to maximize your winnings. Find India’s best Matka Result website here! Get weeklylines game updates along with Date Repair and free Matka Number Guessing Formula. We also provide Morning Syndicate Matka Bazar Syndicate Night Results directly from the Matka industry. Visit us daily for the fastest Matka tips & tricks in our Matka Guessing forum. Don’t forget to bookmark this site for easy access. Thankyou!
Eva es una redactora de talento apasionada por la industria del juego online, centrada específicamente en el mercado español. Ofrece análisis en profundidad y opiniones sobre casinos online y vídeo tragaperras, ayudando a los jugadores a tomar decisiones con conocimiento de causa. Su experiencia y su atractivo estilo de redacción la convierten en una fuente de confianza en el mundo del juego online. Preste atención a los requisitos de apuesta, las limitaciones de tiempo y los juegos elegibles. Si utiliza las bonificaciones de forma eficaz, podrá aumentar sus oportunidades de ganar y aprovechar al máximo su experiencia en Gates of Olympus Xmas 1000. Copy and place the link near the image. If this is if not possible then place it near the footer of the website, blog, newsletter, or credits section.
https://munshimodernpain.com/resena-de-unique-casino-la-experiencia-definitiva-para-jugadores-espanoles/
«Gate of Olympus» es un popular juego de casino online que atrae a jugadores debido a su temática basada en mitologías antiguas y sus múltiples oportunidades de bonificaciones. El juego se estructura en torno a un conjunto de carretes que los jugadores deben girar para alinear símbolos que desencadenen pagos o juegos de bonificación. Consigue símbolos iguales en cualquier lugar y obtén ganancias en Gates of Olympus La volatilidad alta de este slot significa que las ganancias pueden ser menos frecuentes, pero cuando llegan, suelen ser significativas. Esta característica hace que el juego sea ideal para jugadores que buscan emociones fuertes y están dispuestos a esperar por premios grandes. La combinación en Gates of Olympus de alta volatilidad con multiplicadores de hasta 500x crea un potencial explosivo en cada sesión.
Gates of Olympus Gates of Olympus w polskiej wersji językowej to slot, który trzyma w napięciu i oferuje sporo możliwości na duże wygrane. Dzięki bonusom i mnożnikom rozgrywka jest dynamiczna i nieprzewidywalna, co sprawia, że gra się w niego naprawdę dobrze! Aby grać na pieniądze w Gates of Olympus, należy wybierać tylko wiarygodne kasyna. Takie, które oferują tylko licencjonowane oprogramowanie. Gra na prawdziwe pieniądze w Gates of Olympus i inne gry hazardowe, także te z krupierem na żywo, możliwa jest w kasynach po zalogowaniu się. W tym celu musimy utworzyć konto. Czy warto to zrobić? Cóż, hazard to rozrywka jak każda inna – przy zachowaniu zdrowego rozsądku i odpowiedzialnej grze bez wątpienia nie powinno nam przydarzyć się nic złego. Setki tysięcy ludzi w Polsce korzysta z automatów czy zasiada przy stole z ruletką online. Gra na kasę ma tę zaletę, że oferuje znacznie większe emocje. Naturalnie przegrana jest częścią samej gry, ponieważ kasyna online mają zawsze przewagę nad graczem, lecz jeśli nie zechcemy od razu się odegrać, możemy czerpać z tego przyjemność.
https://www.fcevents.com.au/recenzja-verde-casino-nowoczesne-kasyno-online-dla-polskich-graczy/
SlotsUp to informacyjny i wielofunkcyjny projekt w niszy kasyn online, działający od 2015 roku. Mając ponad 10 lat doświadczenia, dostarczamy eksperckie, aktualne i istotne treści, aby pomóc użytkownikom zdecydować, w co grać i gdzie grać – czy w gry darmowe, czy na prawdziwe pieniądze. Nasze recenzje i przewodniki mają charakter wyłącznie informacyjny i nie należy ich uważać za bezpośrednią poradę. Treści SlotsUp są przeznaczone dla użytkowników w wieku 18 lat i starszych lub tych, którzy osiągnęli wiek uprawniający do hazardu w swojej jurysdykcji. Gry slotowe zazwyczaj mają również swoje funkcje specjalne. Wilds to symbole, które mogą zastąpić inne symbole, pomagając tworzyć wygrywające kombinacje.Z kolei Scatters to symbole, które często uruchamiają rundy bonusowe lub darmowe spiny, niezależnie od ich pozycji na bębnach.W wielu slotach można także wygrać bonusowe rundy. Dodatkowe gry w obrębie slotu mogą oferować większe wygrane, darmowe spiny lub interaktywne elementy.
Comment une entreprise, poursuivie des centaines de fois aux prud’hommes, rappelée à l’ordre par les organismes de contrôle, peut-elle continuer à travailler pour les collectivités publiques ? La société Vortex transporte des élèves handicapés aux frais des départements. Une plainte au pénal a été déposée contre ses dirigeants. Premier volet de notre enquête sur la société Vortex. L’ANR met à disposition ses jeux de données sur les projets, cliquez ici pour en savoir plus. Je suis un peu dans le même cas que toi avec le pavé numérique et les flèches. Bien que ce soit plus simple sous Win, je trouve ça un peu pénible de switcher avec la touche verr num et de vérifier le témoin lumineux en cas de doute. Poignée GRIP de rechange 01-2816 Tapez un ou plusieurs mots-clés…
https://hedgedoc.uni-ak.ac.at/s/9RwONMEnx
This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. Pragmatic Play (2015) est salué pour son offre diversifiée, composée des machines à sous en ligne les plus populaires, jeux de table, et même de live casino. Parmi ses plus grands succès figurent Gates of Olympus et Sweet Bonanza, appréciés pour leur gameplay dynamique (avalance et absence de ligne de paiement) et leur taux de volatilité maîtrisé. Les dieux grecs étaient puissants, inconstants et immortels – et Gates of Olympus donne vie à leur monde sur votre ordinateur ou votre appareil mobile. Ce jeu à six rouleaux et cinq rangées est doté d’un système Megaways qui paie partout où les symboles atterrissent, et vous pouvez gagner lorsque vous alignez au moins 12 symboles de grande valeur sur la grille. Vous trouverez des pierres précieuses de moindre valeur et de différentes couleurs, ainsi que des icônes thématiques telles que des anneaux, des sabliers et des coupes. Les symboles de plus grande valeur incluent le puissant Zeus lui-même.
The Astronaut game by 100HP Gaming has become a favorite among players due to its straightforward design and rewarding potential. Several features make it stand out from other crash-style betting games available online. Choose Your Race If the download process has not started automatically, try again. Explore the unexplored. Take on unknown dangers. Build a galactic empire. For the third time in a decade, the winner of Tournament Earth hails from the Canary Islands. NASA explores the unknown in air and space, innovates for the benefit of humanity, and inspires the world through discovery. Is the Astronaut Crash Game app free to use?Yes, downloading and installing the Astronaut app is free, and players can choose between demo mode for practice or switch to real-money mode once they create an account and make a deposit.
https://www.deluxehouses.ae/review-del-juego-balloon-de-smartsoft-diversion-y-ganancias-en-ecuador/
Get ready to discover one of the highest-rated online casinos in Canada, BetVictor Casino, as well as the numerous perks it offers to players. Starburst, Book of Dead, and Mega Moolah are some of the best slots to win real money in 2025, but as well as these titles, our team of casino experts has reviewed hundreds of slots to create the ultimate list of the best slots to play online for real money. Claim up to:рџЋЃ £10000 Bonus🆕 New Casino❌ Non-GamStop➕ £3500 Slots Offerрџ’і Credit Debit Cards AcceptedрџЋ° No Stake Limit on Slotsрџ’ё No Wagering Limit🇬🇧 Players Accepted No Deposit Free Spins for New Players. 100% up to $1,000 + 100FS Welcome. 10% Monthly Cashback While you can deposit more, the more vitamins in your body will be. All slot casino UK these gaming providers are reputable for their quality and innovation in casino gaming, in return.
This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. Entre em contato com o suporte ao cliente e verifique o tempo de resposta, a eficiência e a humanização do processo. Se o site não tiver atendimento em português ou demorar demais para oferecer soluções para possíveis problemas, as chances de que você vá ter dores de cabeça em algum momento do processo serão bem maiores.
https://www.coreoriginator.com/descubra-o-jetx-um-review-completo-do-jogo-da-smartsoft-para-jogadores-brasileiros/
This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. As slots, assim como todos os jogos de cassino online, são criados por desenvolvedoras de jogos responsáveis e de grande credibilidade. Elas são auditadas por empresas independentes que acessam o código-fonte e atestam sua justiça para que os jogadores possam jogar sabendo que podem ganhar e confiar no jogo. A melhor plataforma de 3 reais hoje é a Superbet. Além do depósito baixo, ela traz odds atrativas, tem muitos jogos e suporte ao cliente de qualidade. Veja mais opções de plataforma de jogo que paga aqui!
Your article helped me a lot, is there any more related content? Thanks! https://www.binance.com/id/register?ref=UM6SMJM3
While there is no definitive way to hit a jackpot on Aztec Fire: Hold and Win, several strategies can increase one’s chances: Aztec Fire: Hold and Win is an online slot game that takes players on a journey through the lush jungles of South America in search aztec-fire of lost treasures. The game features stunning graphics and animations, setting it apart from other slots on the market. With five reels and ten paylines, the game offers plenty of opportunities for players to land winning combinations. As European Gaming reports, Yuriy Muratov, Chief Business Development Officer at 3 Oaks Gaming, said: “Aztec Fire 2 is a worthy sequel with the addition of the Unlockable Rows feature being the main differentiator from the original. This slot takes players on a breathtaking jungle journey where they can uncover modifiers and six in-game jackpots, rounding off our 2023 games roadmap in style.”
https://transways-intl.com/2026/01/16/777-casino-review-a-thrilling-experience-for-australian-players/
The Aztec Fire Slot immerses players in the rich tapestry of ancient Mesoamerican culture, where treasures await those brave enough to unlock the secrets hidden within the ruins. This captivating slot machine blends stunning graphics and sound effects with exciting gameplay features to create an unforgettable gaming experience. Players are guided by the spirits of ancient Aztec warriors across a 5-reel, 3-row format. The thrill of the Aztec Fire Slot comes not only from its gameplay but also from its enticing features and bonuses. Here’s a comparative look at some of the prominent features: The Aztec Fire Slot is more than just a game; it’s a captivating experience that combines beautiful graphics, engaging features, and the thrill of potentially lucrative wins. Whether you’re spinning for fun with the aztec fire slot demo or diving into the game with real stakes, the allure of the Aztec world is undeniable.
When you Double Your Jackpot for the Christmas Lotto, winning bets DOUBLE for not just one, not just two, but the THREE highest prizes! Offering no deposit bonuses along with extensive game collections, alluring rewards, diverse payment options, and efficient customer service, the best no deposit bonus casinos have gained a huge following over the past few years. Discover the best free spins no deposit offers in the UK. With +500 bonus reviews, Bojoko is the most trusted source to find no deposit free spins. We showcase the latest slots free spins on this page with expert recommendations and insights. No deposit slots bonuses are available to UK Casino & Slots players who are at least 18 years old and not restricted from the site. These bonuses are typically aimed at new players to encourage trying out games without financial risk.
https://aminallcny.com/neosurf-casino-review-the-go-to-choice-for-australian-players/
When you create videos on CapCut, your videos will not get posted anywhere for others to see. However, the ability to comment and the option to connect to TikTok is where your kid will be the most vulnerable on this app. If I tell you my favorite part of editing in CapCut’s latest Mod version is the Pro Templates & Filters, you’ll know why it is the best video editor for creators like me. These templates, such as birthday templates, travel vlog templates, and wedding highlights templates, save time and improve your video quality up to 4k resolution. You can also explore trending templates to make your videos go viral on Titkok, Meta reels and YouTube shorts. By using the advanced features of CapCut APK, you can effortlessly create eye catching content and keep your audience engaged. Start the development server: bun run dev from (inside apps web)
While the win can still be subject to manipulation, it’s highly unlikely that anyone would go to such great lengths to fake a win so small. $32,255 may not look like much, but it’s not a bad way to start your vacation! Operating a scatter pays win system means Gates of Olympus Super Scatter creates a winning combination when 8 or more matching symbols land anywhere on the grid. Players may wager 20 c to $ €240 per spin, buy free spins or super free spins, and activate an ante bet, where the default RTP when regular betting comes in at 96.5%. The ante bet puts 50% onto the stake when activated to double the chance of triggering the free spins feature. Copyright © 2014-2026 BitStarz. All Rights Reserved. Gates of Olympus 1000 Dice offers a compelling blend of features, including a Scatter Pay system, unlimited Tumble Feature, and striking Multiplier Symbols that can amplify wins significantly, with potential multipliers reaching up to 1,000x. The Free Spins feature enhances play by incorporating cumulative multipliers, while options like Ante Bet and Buy Free Spins provide additional strategic depth, allowing players to increase their chances of winning.
https://zoya.dreamfoodsind.com/aviator-cashbet-how-namibians-can-benefit-2/
Phoenix, 58 x 15 x 15 cm Examined body dissatisfaction, physical attractiveness, and body mass index in adolescents at 13, 15, and 18 years of age. Found that sex differences in body dissatisfaction emerged between 13 and 15 years and were maintained. Girls’ body dissatisfaction increased, whereas boys’ decreased. Body dissatisfaction was weakly related to others’ rating… The lurch between the two worlds is incredibly invigorating, the contrast ofold Europe and young Australia lifts your ability to embrace more of what you want in your work. I’ve had the wonderful advantage of visiting some of the most wonderful museums in the world and I can cherry pick from the best exhibitions, Australia and Europe has to offer. Last year I was fortunately enough to be selected as one of the artists to be part of the The Australian Print Council Print Commission. I have attended and been a part of two IMPACT Conferences in Melbourne and Dundee Scotland. I have built up connections by attending and being part of the SGCI Conferences in the USA. Last year I also attended the Eighth Australian Print Symposium in Canberra, Australia. When travelling I like to visit different Studios, for example the East London Printmakers and the Kathy Caraccio Printing Studio in New York. Recently, I had a Canadian printmaker from the Kamloops Printmakers group, Linda Jules, stay with me.
Also known as grid slots, Cluster Pays slots are on the rise. All slot studios now offer slot games with the Cluster Pays mechanic. In my in-depth guide, I look at what Cluster Pays is, how payouts or winning combinations are formed, what you can expect and the bonus features you’ll encounter. Youll notice that some of them are grouped, just load the title you wish to play in demo mode. The sites have responded by releasing exciting new games and features, when and where to play aloha! cluster pays and of course. But what really comes across as an unexpected surprise is the games music, well answer all your questions and show you the list of the best free keno games – so don’t waste your time. When and where to play aloha! cluster pays for example, read this short article. The country has great tourist destinations to tour during the day, and become a keno expert.
https://www.saffron5206.com/jokaroom-casino-game-review-a-top-choice-for-australian-players/
Yes, you can play Aloha! Cluster Pays on a mobile device, as well as tablet or desktop devices. As long as you are equipped with reliable internet connection, you can start playing on your mobile device from anywhere you are! Gambling games are created to provide a source of amusement, and should be enjoyed in moderation. We remind the clients so you can gamble responsibly, and we render some products and you can information so you can remain on track. To get expertise on the local casino’s reputation, take the time to peruse ratings and you can testimonials away from fellow players. Confident feedback off their gamblers functions as an invaluable indication away from the brand new gambling enterprise’s condition and trustworthiness inside gambling area. India’s Best Online Casino Slot & Live Games
When you had enough practice, and you are ready for the Gates of Olympus real money mode, we suggest you take a look at our list of best free slot games to play. All those operators offer the Gates of Olympus online slot in their libraries to be played in real money mode. The Gates of Olympus slot is no ordinary Greek mythology slot game. This thunder-charged epic features Tumbling Reels and divine Multipliers that can summon stunning wins in both the base game and the Free Spins Round. Fueled by Pragmatic Play’s trademark visuals and animations, it’s a reel forged in the fires of Hephaestus and definitely worth a spin or two. Connect with us COPYRIGHT © 2015 – 2025. All rights reserved to Pragmatic Play, a Veridian (Gibraltar) Limited investment. Any and all content included on this website or incorporated by reference is protected by international copyright laws.
https://sistemamultiplica.com.br/sunspin-casino-review-for-australian-players/
Lucky Carnival Casino is a sensational non-GamStop casino with Big Bass Bonanza. The site is very new and fresh, but it’s so easy to navigate and the design is splendid. Mobile bettors will love that you can download an app for your phone, meaning you can enjoy slots and thousands of other games whenever you like. SlotsOnlineCanada is your favourite online slots website, providing helpful guides, how-to-play guides, casino recommendations and information for players in Canada and worldwide. We’re on a mission to create Canada’s best online slots portal using innovative technology and access to regulated gambling brands. Please play responsibly. Winning when playing the Big Bass Bonanza online slot is as easy as lining up between three and five matching symbols. You can land lots of small and medium wins, while high-paying float symbols can land you a top prize of 20,000 coins.
Besides offering a wide variety of betting options, Goldrush offers some of the best odds available in the sports market and a wide variety of sports. If you’re looking for something a little different than sport to bet on, you can take a wager in the Special Bets section, where topics such as politics, space, rockets and BBC Personality of the Year, and much more are available. We also have a 200% multi -leg stake. Would be 0 if could.horrible customer service,horrible app,laddbucks is complete fix and now takes almost 6 weeks to gain 3 spins.bet365 the way Won $3,520 on Super Stake Roulette (Bet IDs 227497004657 and 227531149921). Support confirmed case escalation but no payout or case number after 4 days. Full documentation sent to regulator and bank.” Wing Roulette Platter Fridays | Here is a guide to winning at online slot machines
https://www.jadranenergetika.si/ripper-casino-login-the-aussie-gateway-to-200-free-spins-bonanza-2026/
Inspiration for Aloha: Cluster Pays seems to have come from Hawaii and from the Tiki gods which you can see in the statues and masks which are still present on the islands. The Hawaiian themed Aloha! Cluster Pays is Netent’s third release in 2016Given the high standards of the first two releases of 2016, Guns N’ Roses and Drive: Multiplier Mayhem, expectations were very high. In this review, we will check the games features, design, payout possibilities and see where you can play it right now and get a nice juicy casino welcome bonus. The best cluster pays slots are Reactoonz, Jammin’ Jars, and Aloha! Cluster Pays. These include exciting features and engaging visuals. You can read more about these and other highly rated cluster pays games at the start of this page. Another cool Hawaiin style bonus feature is the free spin symbol Aloha Slot has on offer. This symbol may come up on any point of the reel and can offer up to 12 free spins if 6 of these matching symbols are displayed. Reveal just 3 and you could still land 9 free spins.
Dork Unit çevrimiçi slot oyunudur. Hem eğlendirir hem de kazanç sağlar. İki türü vardır: biri çok bonus sunar, diğeri ise daha fazla ödül verir. Bu farkı kavramak önemlidir. En iyisini bulmak için demo oyununu deneyebilirsiniz. Bu versiyon size bonusları, wild sembolleri ve çarpanları gösterecek. Ayrıca, bir satın alma özelliği de mevcuttur. Bu özellikleri kullanarak nasıl kazanacağınızı öğrenebilirsiniz. Dork Unit, eğlenceli ve ödüllendirici bir slot oyunu arayan herkes için idealdir. Bir çok oyuncu için en iyi seçeneklerden biri olarak öne çıkar. Dork Unit, eğlenceli ve ödüllendirici bir slot oyunu arayan herkes için idealdir. Bir çok oyuncu için en iyi seçeneklerden biri olarak öne çıkar. Dork Unit çevrimiçi slot oyunudur. Hem eğlendirir hem de kazanç sağlar. İki türü vardır: biri çok bonus sunar, diğeri ise daha fazla ödül verir. Bu farkı kavramak önemlidir. En iyisini bulmak için demo oyununu deneyebilirsiniz. Bu versiyon size bonusları, wild sembolleri ve çarpanları gösterecek. Ayrıca, bir satın alma özelliği de mevcuttur. Bu özellikleri kullanarak nasıl kazanacağınızı öğrenebilirsiniz.
https://iraqrivers.click/2026/02/05/pinco-casino-alt-ust-bahisleri-ile-stratejiler/
RESTAURANT, CINEMA, NIGHT CLUB Sosyal Medya Yönetimi Bu slot, Türkiye’deki casino oyuncuları arasında en tanınan ve tercih gören slotlardan biridir. Bunun esas nedeni, oyunun yüksek getirili yapısı ve Pragmatic Play’in sağlam altyapısıyla hazırlanmasıdır. Türk kullanıcılar, özellikle kazandıran tumble yapısı ve büyük multiplier ödülleri sebebiyle, Gates of Olympus’u tempolu oyun sevenler arasında baş köşeye koyar. Clear the Grid Prize, tüm sembolleri temizledikten sonra gelir. Kazancınız, toplam bahsin 50 katına kadar olabilir. Ücretsiz dönüşler, Trinity özelliği ile temizlene sembollerde başlar. 2025’te abiye modasında sofistike tonlar ve iddialı desenler ön planda. Klasik siyah ve gece mavisinin yanı sıra zümrüt yeşili, vişne çürüğü ve metalik tonlar öne çıkan renkler arasında. Florallar, payetli desen geçişleri ve degrade kumaşlar da trendlerde yerini alıyor. Canlı renkler cesur stilleri, pastel tonlar ise zarif ve romantik bir görünümü yaratıyor.